Question

Calculate the sample mean and sample variance for the following frequency distribution of heights in centimeters for a sample of 8-year-old boys. If necessary, round to one more decimal place than the largest number of decimal places given in the data.

Heights in Centimeters
Class Frequency
121.6-125.2 31125.3-128.9 46129.0-132.6 40132.7-136.3 46136.4-140.0 19

Answer 1

`\bar X = (\sum_(i=1)^n x_i f_i)/(\sum_(i=1)^n f_i)= (23716.8)/(182)= 130.312 \approx 130.3`

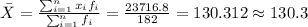
And the variance can be calculated with this formula:

`s^2 = (\sum fx^2 - ((\sum x f)^2)/(n))/(n-1)`

And replacing we got:

`s^2 = (3094539.88 -((23716.8)^2)/(182))/(181)=21.85 \approx 21.9`

Explanation:

For this case we can calculate the mean with the following table:

Class Midpoint (xi) fi xi *fi xi^2 *fi

121.6- 125.2 123.4 31 3825.4 472054.36

125.3-128.9 127.1 46 5846.6 743102.86

129.0-132.6 130.8 40 5232 684345.6

132.7-136.3 134.5 46 6187 832151.5

136.4-140.0 138.2 19 2625.8 362885.56

____________________________________________

Total 182 23716.8 3094539.88

And we can calculate the mean with the following formula

`\bar X = (\sum_(i=1)^n x_i f_i)/(\sum_(i=1)^n f_i)= (23716.8)/(182)= 130.312 \approx 130.3`

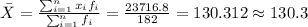
And the variance can be calculated with this formula:

`s^2 = (\sum fx^2 - ((\sum x f)^2)/(n))/(n-1)`

And replacing we got:

`s^2 = (3094539.88 -((23716.8)^2)/(182))/(181)=21.85 \approx 21.9`