Equation of a line that is perpendicular to given line is
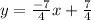 .
.
Equation of a line that is parallel to given line is
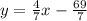 .
.
Solution:
Given line
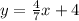 .
.
Slope of this line,
 =
=

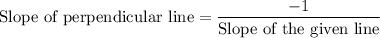
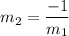
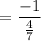
Slope of perpendicular line,
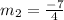
Passes through the point (–7, 5). Here
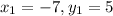 .
.
Point-slope formula:

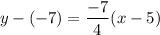
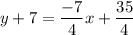
Subtract 7 from both sides, we get
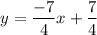
Equation of a line that is perpendicular to given line is
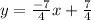 .
.
To find the parallel line:
Slopes of parallel lines are equal.

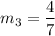
Passes through the point (–7, 5). Here
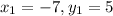 .
.
Point-slope formula:
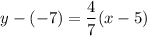

Subtract 7 from both sides,
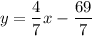
Equation of a line that is parallel to given line is
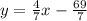 .
.