Question

The equation y 4.9t 2 3.5t 2.4 relates the height y in meters to the elapsed time t in seconds for a ball thrown downward at 3.5 meters per second from a height of 2.4 meters from the ground In how many seconds will the ball hit the ground Express your answer as a decimal rounded to the nearest hundredth

Answer 1

`t \approx 0.43\,s`

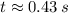
Explanation:

The vertical displacement function is
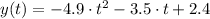`y(t) = -4.9\cdot t^(2)-3.5\cdot t + 2.4`, where
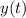`y(t)` is measured in meters and
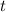`t` in seconds. Ball hits the ground when
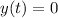`y(t) = 0`. That is:

`-4.9\cdot t^(2)-3.5\cdot t + 2.4 = 0`

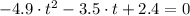
Whose roots can be found by using the General Formula for Second-Order Polynomials:

`t_(1,2) = \frac{3.5\pm \sqrt{(-3.5)^(2)-4\cdot (-4.9)\cdot (2.4)} }{2\cdot (-4.9)}`

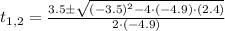
Solutions of this polynomial are:

`t_(1) \approx 0.43\,s,t_(2) \approx -1.14\,s`

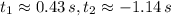
Only the first root is physically consistent.