Question

The relationship between the number of calculators x a company sells per day and the price of each calculator p is given by the equation x = 2300 − 100 p . At what price should the calculators be sold if the daily revenue is to be $ 6 , 000 ? Remember, revenue (R) is the product of price (p) and items sold (x), in other words, R = x p .

Answer 1

The price should be either $3 or $20.

Explanation:

The relationship between the number of calculators sold, x and the price p is given by two equations. R reffers the revenue of the company.

1. x = 2300 - 100p.
2. R = xp or, 6000 = xp or,
   `x = (6000)/(p)`.

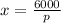Now, putting the value of the second equation in first equation, we get

`x = 2300 - 100p\\(6000)/(p) = 2300 - 100p\\60 = 23p - p^(2) \\p^(2) - 23p + 60 = 0\\p^(2) - 20p - 3p + 60 = 0\\(p - 20)(p - 3) = 0.\\p = 20, 3`.

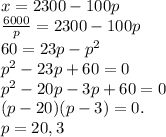The price is either $3 or $20.