Answer: b. (0.561, 0.794).
Explanation:
We know that the confidence interval for population proportion (p) is given by:-
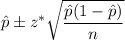
, where
 = Sample proportion.
= Sample proportion.
n = Sample size.
z* = Critical z-value.
Let p = proportion of horses with enteroliths who are fed at least two flakes of alfalfa per day.
As per given , n = 62
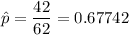
z-value for 95% confidence = z*=1.96
A 95% confidence interval is given by:

Thus , the required 95% confidence interval is (0.561, 0.794).
Hence, the correct option is b. (0.561, 0.794)..