Question

Five-gram samples of copper and aluminum are at room temperature. Both receive equal amounts of energy due to heat flow. The specific heat capacity of copper is 0.09 cal/g°C, and the specific heat capacity of aluminum is 0.22 cal/g°C. Which of the following statements is true?

a. The temperature of each sample increases by the same amount.
b. The aluminum will get hotter than the copper.
c. The copper will get hotter than the aluminum.
d. The temperature of each sample decreases by the same amount

Answer 1

• c. The copper will get hotter than the aluminum.

Step-by-step explanation:

The energy due to heat flow, i.e. the heat energy, is proportional to the product of the mass, the specific heat capacity, and the change in temperature:

`Heat=mass* \text{specific heat capacity }*\Delta T`

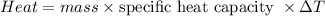
From which you obtain:

`\Delta T=\frac{Heat}{mass* \text{specific heat capacity}}`

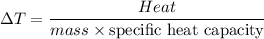
That equation tells that the change in temperature is inversely related to the product of the mass and the specific heat.

In the problem, the masses of the samples of copper and aluminum are equal (5.00g) and both samples receive equal amounts of energy due to heat flow, thus the only difference is the specific heat capacity of each sample.

From the above stated relationship between the change in temperature, the heat, the mass, and the specific heat capacity, under the assumption of all the other conditions equal (heat energy and mass), the higher the specific heat capacity the lower the change in temperature, and the lower the specific heat capacity the greater the change in temperature.

The heat capacity of copper (0.09 cal/g°C) is lower than the specific heat capacity of aluminum is (0.22 cal/g°C), thus the increase in temeperature of the copper sample will be greater than that of the aluminum sample. This means that the copper will get hotter than the aluminum (option c.)