Question

A simple random sample consists of 65 lengths of piano wire that were tested forthe amount of extension under a load of 30 N. The average extension for the 65 lines was 1.102mm and the standard deviation (sample) was 0.020 mm. Let µ represent the mean extensionfor all specimens of this type of piano wire.

(a) Assuming a significance level of α = 0.05, determine the critical value for testing

H0 : µ ≤ 1.1 vs HA : µ > 1.1.


(b) Find the test statistics and p-value for the previous test. (An approximation of the p-value using a t-table is sufficient)
(c) State the conclusion of the previous test.

Answer 1

a) For this condition (α=0.05, df=64, one-sided test), the critical value is t=1.669.

b) The P-value is 0.46

c) The null hypothesis can not be rejected

Explanation:

The null and alternative hypothesis are:

`H_0: \mu \leq 1.1 \\\\H_a: \mu > 1.1`

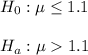
The significance level is α=0.05.

The degrees of freedom are 64.

The standard deviation of the sample is 0.02 mm.

For this condition (α=0.05, df=64, one-sided test), the critical value is t=1.669.

The test statistic t is calculated as:

`t=(M-\mu)/(s_m)=(1.102-1.100)/(0.020) =(0.002)/(0.020)=0.1`

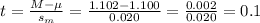
As t=0.1 belong to the acceptance region, the null hypothesis can't be rejected.

The P-value is 0.46, and it is bigger than the level of significance. The conclusion is the same: the null hypothesis can not be rejected as there is no strong evidence against it.