Answer:
Explanation:
Hello!
The variable of interest in this exercise is:
X: number of orders that are done wrong out of 700.
This is a discrete variable with a binomial distribution. The parameter of the study is the proportion of orders done wrong at the fast-food restaurant.
Considering that n≥30, n*p≥5 and n*q≥5 you can apply the Central Limit Theorem and approximate the distribution of the sample proportion, p', to normal. Doing so you can construct the Confidence Interval using an approximation to the standard normal distribution:
p'= 242/700= 0.35
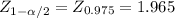
p' ±
 *
*
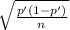
0.35 ± 1.965 +
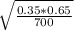
(0.31;0.39)
With a confidence level of 95%, you'd expect that the interval (0.31;0.39) includes the true proportion of incorrect orders of the fast-food restaurant.
I hope it helps!