It is yes for ordered pairs 1 and 4. It is no for ordered pairs 2 and 3.
Explanation:
Step 1:
The given equations are multiples of each other so they have an infinite number of solutions.
So we need to substitute the values of x and y in the equations to determine which ordered pairs are solutions to the given equations.
Step 2:
When (x, y) = (7, 11),
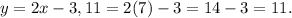
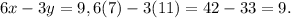
So the first ordered pair is a solution to the given system of equations.
When (x, y) = (4, -5),
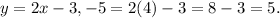
-5 ≠ 5,
So the second ordered pair is not a solution.
Step 3:
When (x, y) = (-1, 8),
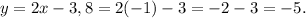
8 ≠ -5,
So the third ordered pair is not a solution.
When (x, y) = (0, -3),
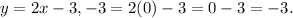
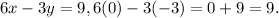
So the fourth ordered pair is a solution to the given system of equations.