Question

For alloys of two hypothetical metals A and B, there exist an ?, A-rich phase and a ?, B-rich phase.

From the mass fractions of both phases for two different alloys (given below), which are at the same temperature, determine the composition of the phase boundary (or solubility limit) for the following:

alloy composition fraction \alpha phase fraction \beta phase
60 wt% A - 40 wt% b 0.59 0.41
30 wt% A - 70 wt% b 0.14 0.86

Answer 1

Alpha Boundary contains 87.33% of A and 12.66% of B

Beta Boundary contains 20.67% of A and 79.33% of B

Step-by-step explanation:

For the two alloys with composition as given in the question the values of the Weightage is given as

`W_a_1=(C_(\beta)-C_o_1)/(C_(\beta)-C_(\alpha))`

Here

Wa1 os given as 0.59 as value of Alpha Phase for 1st Alloy

Co1 is given as 60% for the first Alloy so the equation becomes

`W_a_1=(C_(\beta)-C_o_1)/(C_(\beta)-C_(\alpha))\\0.59=(C_(\beta)-60)/(C_(\beta)-C_(\alpha))\\0.59C_(\beta)-0.59C_(\alpha)=C_(\beta)-60\\C_(\beta)-60-0.59C_(\beta)+0.59C_(\alpha)=0\\0.41C_(\beta)+0.59C_(\alpha)-60=0`

Similarly for the 2nd alloy

`W_a_2=(C_(\beta)-C_o_2)/(C_(\beta)-C_(\alpha))`

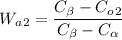
Here

Wa2 os given as 0.14 as value of Alpha Phase for 1st Alloy

Co1 is given as 30% for the first Alloy so the equation becomes

`\geq W_a_2=(C_(\beta)-C_o_2)/(C_(\beta)-C_(\alpha))\\0.14=(C_(\beta)-30)/(C_(\beta)-C_(\alpha))\\0.14C_(\beta)-0.14C_(\alpha)=C_(\beta)-30\\C_(\beta)-30-0.14C_(\beta)+0.14C_(\alpha)=0\\0.86C_(\beta)+0.14C_(\alpha)-30=0`

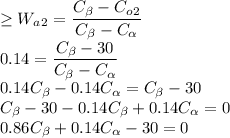
Solving the two equations as

`0.41C_(\beta)+0.59C_(\alpha)-60=0\\0.86C_(\beta)+0.14C_(\alpha)-30=0\\C_(\beta)=20.67\%\\C_(\alpha)=87.33\%`

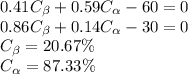
So the boundaries are as

Alpha Boundary contains 87.33% of A and 12.66% of B

Beta Boundary contains 20.67% of A and 79.33% of B