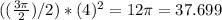Answer:
Area of the sector =
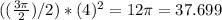
Explanation:
Remember that the formula for the area of a circular sector is given by
Area of a circular sector =
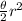
Where
 is the angle measures in radians, and
is the angle measures in radians, and
 is the radius of the circle.
is the radius of the circle.
For our problem
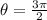
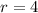
Therefore Area of the sector =