Question

A 23.0 kg child plays on a swing having support ropes that are 2.10 m long. A friend pulls her back until the ropes are 45.0 degree from the vertical and releases her from rest. What is the potential energy for the child as she is released, compared with the potential energy at the bottom of the swing? How fast will she be moving at the bottom of the swing? How much work does the tension in the ropes do as the child swings from the initial position to the bottom?

Answer 1

a. 139.748J

b.3.486m/s

c.zero

Step-by-step explanation:

a. Given the mass of the child as 23.0kg, rope length is 2.1mand incline is 45°

Potential energy during release is calculated as:
`PE=mgh`

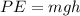
#Find vertical difference of when the swing is at rest (2.1m) and when the child is pulled back.

Find the height when the child is pulled back:

`cos 45\textdegree=y/2.10\\\\y=1.48m`

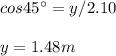
#therefore,vertical difference is 2.1m-1.48m=0.62m

`\therefore PE=mgh\\\ \ =23.0kg* 9.8m/s^2* 0.62m\\\ \ =139.748J`

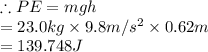
#Hence the potential energy during release is 139.748J

b. From a, above, we have PE=139.748J, M=23.0kg.

At the bottom, all the PE will be transferred into KE. Potential energy is calculated as:

`KE=0.5mv^2\\\\mv^2=2KE\\\\v=√(2KE/m)\\\\v=√(2* 139.748J/23.0)\\\\v=3.486m/s`

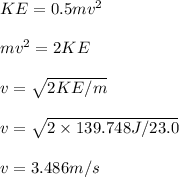
#Hence the velocity at the bottom of the swing is 3.486m/s

c. Work is calculated as the product of force by distance.

From a, b above we have mass as 23.0kg .

-since the distance of the ropes remained constant the change in distance is zero:

`W=mgd\\=23.0* 9.8m/s^2* 0\\=0`

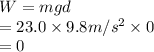
Therefore the work in the ropes is 0,zero.