Question

Suppose a child walks from the outer edge of a rotating merry-go round in towards the center of rotation. Does the angular velocity of the merry-go-round increase, decrease, or remain the same?

Answer 1

Increases.

Step-by-step explanation:

Angular velocity is defined as the time rate of change of the distance of the circular motion in rad/s.

As the child walks from the outer edge to the center, the moment of inertia, I is the sum of the moment of inertia of the merry go round and the child.

As the child walks inwardly, the moment of inertia decreases and so the net moment of inertia decrease. Hence, final angular velocity increases.

The final angular velocity can be calculated from the definition of angular momentum,

L = Iω.

Answer 2

final angular speed will be more than initial speed as child moves inside

Step-by-step explanation:

So here as the child and Merry go round is an isolated system so there is no external Torque on this system from outside

As here we can see there is external force acting on this system by the hinge of the Merry go round as well as due to gravity so we can not use momentum conservation to solve such type of questions.

But as we can say that there is no external torque on this system about the hinge point so we will use conservation of angular momentum for this system

Here as we know that

`\tau = (dL)/(dt)`

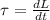
where L = angular momentum

since here torque is ZERO

`0 = (dL)/(dt)`

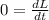
L = constant

so here we can write initial angular momentum of the system as

`L = (I_1 + I_2)*\omega`

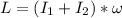
here we know that

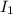`I_1`= moment of inertia of merry go round

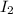`I_2` = moment of inertia of child

so here we can say

`(I_1 + I_2)* \omega_1 = (I_1 + I_2')\omega_2`

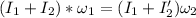
so here as the child moves from edge to inside the disc it moment of inertia will decrease because as we know that moment of inertia of child is given as

`I_2 = mr^2`

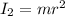
here m = mass of child

r = distance of child from center

Since child is moving inside so his distance from center is decreasing

so here moment of inertia of child is decreasing as he starts moving inside

so final angular speed of merry go round will increase as child go inside
`\omega_2 = ((I_1 + I_2)*\omega)/((I_1 + I_2'))`

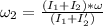
so here as

`I_2' < I_2`

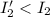
final angular speed will be more than initial speed as child moves inside