Question

A map is laid out in the standard (x,y) coordinate plane. How long, in units, is an airplane's path on the map as the airplane flys along a straight line from City A located at (20,14) to City B located at (5,10)

Answer 1

Distance between the points A and B is 15.52 units.

Explanation:

It has been given in the question that an airplane flies along a straight line from City A to City B.

Map has been laid out in the (x, y) coordinate plane and the coordinates of these cities are A(20, 14) and B(5, 10).

Distance between two points A'(x, y) and B'(x', y') is represented by the formula,

d =
`\sqrt{(x-x')^(2)+(y-y')^(2)}`

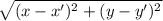
So we plug in the values of (x, y) and (x', y') in the formula,

d =
`\sqrt{(20-5)^(2)+(14-10)^(2)}`

d =
`\sqrt{(15)^(2)+(4)^(2)}`

d =
`√(225+16)`

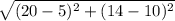
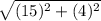
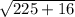
d = 15.52

Therefore, distance between the points A and B is 15.52 units.