Answer:
The velocity of the arrow after 3 seconds is 30.02 m/s.
Step-by-step explanation:
It is given that,
An arrow is shot upward on the moon with velocity of 35 m/s, its height after t seconds is given by the equation:
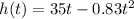
We know that the rate of change of displacement is equal to the velocity of an object.
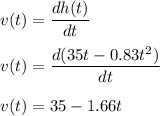
Velocity of the arrow after 3 seconds will be :

So, the velocity of the arrow after 3 seconds is 30.02 m/s. Hence, this is the required solution.