Question

The monthly cost of driving a car depends on the number of miles driven. Lynn found that in May her driving cost was $380 for 480 mi and in June her cost was $450 for 830 mi. Assume that there is a linear relationship between the monthly cost C of driving a car and the distance x driven. Find a linear equation that relates C and d.

Answer 1

`y=0.2x+284`

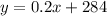
Explanation:

Let x be the distance driven, d-distance and C our constant.

Our information can be presented as:

`y=mx+c\\\\450=830x+C\ \ \ \ \ \ \ \ \ eqtn 1\\\\380=480x+C\ \ \ \ \ \ \ \ \ eqtn 2`

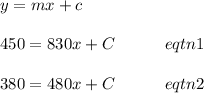
#Subtracting equation 2 from 1:

`70=350x\\x=0.2`

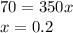
Hence the fixed cost per mile driven,
`x` is $0.20

To find the constant,
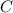`C` we substitute
`x` in any of the equations:

`450=830x+C\ \ \ \ \ \ \ X=0.2\\\therefore C=450-830*0.2\\=284`

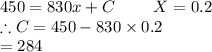
Now, substituting our values in the linear equation:

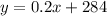`y=0.2x+284` #y=cost of driving, x=distance driven

Hence the linear equation for the cost of driving is y+0.2x+284