Question

A spring hangs from the ceiling with an unstretched length of x 0 = 0.35 m . A m 1 = 6.3 kg block is hung from the spring, causing the spring to stretch to a length x 1 = 0.50 m . Find the length x 2 of the spring when a m 2 = 3.7 kg block is hung from the spring. For both cases, all vibrations of the spring are allowed to settle down before any measurements are made.

Answer 1

x₂=0.44m

Step-by-step explanation:

First, we calculate the length the spring is stretch when the first block is hung from it:

`\Delta x_1=0.50m-0.35m=0.15m`

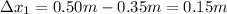
Now, since the stretched spring is in equilibrium, we have that the spring restoring force must be equal to the weight of the block:

`k\Delta x_1=m_1g`

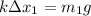
Solving for the spring constant k, we get:

`k=(m_1g)/(\Delta x_1)\\\\k=((6.3kg)(9.8m/s^(2)))/(0.15m)=410(N)/(m)`

Next, we use the same relationship, but for the second block, to find the value of the stretched length:

`k\Delta x_2=m_2g\\\\\Delta x_2=(m_2g)/(k)\\\\\implies \Delta x_2=((3.7kg)(9.8m/s^(2)))/(410N/m)=0.088m`

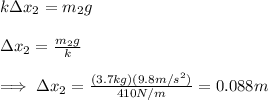
Finally, we sum this to the unstretched length to obtain the length of the spring:

`x_2=0.35m+0.088m=0.44m`

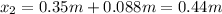
In words, the length of the spring when the second block is hung from it, is 0.44m.