Question

A rectangular solid with a square base has a volume of 2,744 cubic inches. (Let w represent the length of the sides of the square base and let h represent the height of the solid.) (a) Determine the dimensions (in inches) that yield the minimum surface area.

Answer 1

For minimum surface area, the base length and height are equal in length and equal to 14 inches.

Explanation:

Given:

Volume of rectangular solid (V) = 2744 cubic inches

Length of base side = 'w'

Height of solid = 'h'

We know that,

Volume = Area of base × Height

`2744=(w* w)* h\\\\2744=w^2h\\\\h=(2744)/(w^2)-----(1)`

Now, surface area of the solid is given as:

`Surface\ area=2* (base\ area)+4(hw)\\\\Surface\ area=2w^2+4hw`

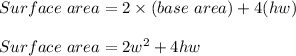
Plug in 'h' value from equation (1). This gives,

`Surface\ area=2w^2+4*(2744w)/(w^2)\\\\Surface\ area=2(w^2+(5488)/(w))`

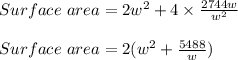
Now, for minimum surface area, the derivative of surface area with respect to length 'w' must be 0.

Differentiating both sides with respect to 'w' and equating it to 0, we get:

`(dS)/(dw)=0\\\\(d)/(dw)[2(w^2+(5488)/(w))]=0\\\\2w-(5488)/(w^2)=0\\\\2w=(5488)/(w^2)\\\\w^3=(5488)/(2)\\\\w=\sqrt[3]{2744}= 14\ in`

Therefore, the base length is 14 inches.

Now, from equation (1), the height is given as:

`h=(2744)/(w^2)\\\\h=(2744)/(14^2)=14\ in`

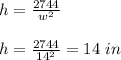
Therefore, for minimum surface area, the base length and height are equal in length and equal to 14 inches.