Question

Mai drove to the mountains last weekend. There was heavy traffic on the way there, and the trip took 8 hours. When Mai drove home, there was no traffic and the trip only took 6 hours. If her average rate was 16 miles per hour faster on the trip home, how far away does Mai live from the mountains?

Answer 1

Mai lives 384 miles away from the mountains

Explanation:

Let d represent distance between Mai's house and mountains and r represent Mai's rate while going to mountains.

We have been given that there was heavy traffic on the way there, and the trip to mountains took 8 hours.

`\text{Distance}}=\text{Time}* \text{Speed}`

`d=8r...(1)`

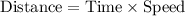
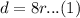
We are also told that when Mai drove home, there was no traffic and the trip only took 6 hours. Her average rate was 16 miles per hour faster on the trip home.

`d=6(r+16)...(2)`

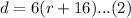
Upon equating equation (1) and equation (2), we will get:

`8r=6(r+16)`

`8r=6r+96`

`8r-6r=6r-6r+96`

`2r=96`

`(2r)/(2)=(96)/(2)`

`r=48`

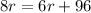
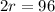
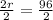
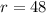
Upon substituting
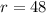`r=48` in equation (1), we will get:

`d=8r\Rightarrow 8(48)=384`

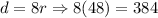
Therefore, Mai lives 384 miles away from the mountains.