Question

Three resistors having resistances of R1 = 1.84 Ω , R2 = 2.28 Ω and R3 = 4.75 Ω respectively, are connected in series to a 28.5 V battery that has negligible internal resistance.

Part A) Find the equivalent resistance of the combination.Part B) Find the current in each resistor.Answer in the order indicated. Separate your answers using commas.IR1,IR2,IR3 =Part C) Find the total current through the battery.Part D) Find the voltage across each resistor.

Answer 1

a. 0.8385 Ω

b.

`I_(1.84)15.50A\\\\I_(2.28)=12.5A\\\\I_(4.75)=6.0A`

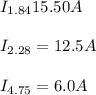
c.34.0A

d.28.5V

Step-by-step explanation:

a. The 3 resistors are connected in parallel. To get the equivalent resistance
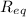`R_e_q`, we calculate the combinations in parallel,

-Their combinations is:

`(1)/(R_e_q)=(1)/(R_(1.84))+(1)/(R_(2.28))+(1)/(R_(4.75))\\\\(1)/(R_e_q)=(1)/(1.84\Omega )+(1)/(2.28\Omega )+(1)/(4.75\Omega )\\\\(1)/(R_e_q)=(1)/(1.192601)\\\\R_e_q=0.8385\Omega`

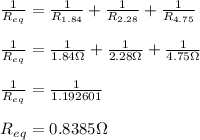
#Hence the equivalent resistance of the combination is 0.8385 Ω

b. The 3 resistors are connected in parallel. This means the current is not the same for the 3 resistors. We can use Ohm's law to get current for each resistor, where the voltage for the three is 28.5 V:

`I_(1.84)=(28.5)/(1.84\Omega)=15.50A\\\\I_(2.28)=(28.5)/(2.28\Omega)=12.5A\\\\I_(4.75)=(28.5)/(4.75\Omega)=6.0A`

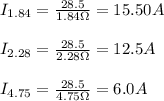
Hence the current for the three resistors is 15.50A(1.84Ω), 12.5A(2.28Ω), 6.0A(4.75Ω)

c. The total current through resistors connected in parallel is the sum of the individual current flowing through each resistor:

I=15.50A+12.50A+6.0A=34A

#Hence,the total current through the battery is 34.0A

d. Since the three resistors are connected in parallel with the battery, the potential difference across them is same for every resistor and equals the potential difference across the combination:

`\epsilon=V_(1.84)=V_(2.28)=V_(4.75)=28.5V`

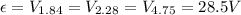
#Hence the voltage across each resistor. is 28.5V