Question

A pulsar is a rapidly rotating neutron star that emits a radio beam the way a lighthouse emits a light beam. We receive a radio pulse for each rotation of the star. The period T of rotation is found by measuring the time between pulses. The pulsar in the Crab nebula has a period of rotation of T = 0.033 s that is increasing at the rate of

1.26×10−5s/y
. (a) What is the pulsar’s angular acceleration α? (b) If α is constant, how many years from now will the pulsar stop rotating? (c) The pulsar originated in a supernova explosion seen in the year 1054. Assuming constant α, find the initial T.

Answer 1

α
`= -2.303 * 10^-^9rad/s^2`

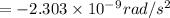
b)t = 2619.8 years

c) T(i) = 0.0208536s

Step-by-step explanation:

Given that ,

The period of pulsar T = 0.033 s

The period increase at a rate of
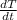`(dT)/(dt)` = 1.26×10⁻⁵s/y

a) Pulsar angular speed is

ω = θ / T = 2π / T

θ = one revolution of pulsar

T = period of pulsar

Pulsar angular acceleration is given by

`\alpha = (dw)/(dt)`

`\alpha = -(2\pi )/( T^2)(dT)/(dt)`

`\alpha = -(2\pi )/(0.033^2) (1.26 * 10^-^5)/(60*60*24*365.25)`

`= -2.303 * 10^-^9rad/s^2`

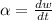
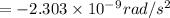
b) ω₀ = θ / T

0 = 190.4 - 2.303 × 10⁻⁹

`t = (190.4 )/(2.303 *10^-^9) \\= 8.27 *10^1^0s \\= 2619.8y`

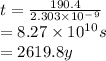
c) 2018 - 1054

= 964years

The pulsar is originated in a supernova explosion 964 years ago.

then the initial period of pulsar

`T_i = T - 964 * (dT)/(dt) = 0.033 - 964 * 1.26 * 10^-^5 \\= 0.0208536s`

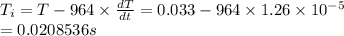
T(i) = 0.0208536s