Answer:
144 sq in
Explanation:
Face height=9, bases=6 in
#Assume the pyramid has a square base.
First we need to calculate the perpendicular height of the pyramid:
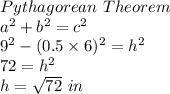
Now to find the surface area of each pyramid:
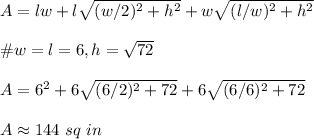
Hence amount of construction paper needed to make each pyramid is 144 sq in