The second term of the expansion is
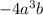 .
.
Solution:
Given expression:
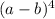
To find the second term of the expansion.
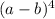
Using Binomial theorem,
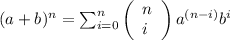
Here, a = a and b = –b
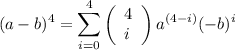
Substitute i = 0, we get
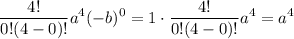
Substitute i = 1, we get
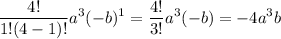
Substitute i = 2, we get
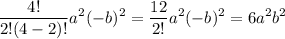
Substitute i = 3, we get
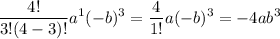
Substitute i = 4, we get
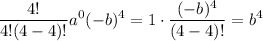
Therefore,
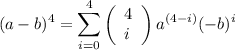
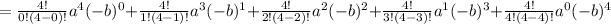
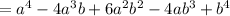
Hence the second term of the expansion is
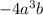 .
.