Question

Suppose that, on average, electricians earn approximately μ= $54,000 per year in the united states. Assume that the distribution for electricians' yearly earnings is normally distributed and that the standard deviation is σ= $12,000. What is the probability that the sample mean is greater than $66,000?

Answer 1

0.15866.

Explanation:

We have been given that on average, electricians earn approximately μ= $54,000 per year in the united states. Assume that the distribution for electricians' yearly earnings is normally distributed and that the standard deviation is σ= $12,000. We are asked to find the probability that the sample mean is greater than $66,000.

First of all, we will find the z-score corresponding to 66,000 using z-score formula.

`z=(x-\mu)/(\sigma)`

`z=(66000-54000)/(12000)`

`z=(12000)/(12000)`

`z=1`

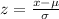
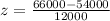
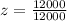
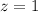
Now, we need to find the probability that z-score is greater than 1 that is
`P(z>1)`.

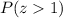Upon using formula
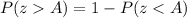`P(z>A)=1-P(z<A)`, we will get:

`P(z>1)=1-P(z<1)`

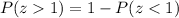
Upon using normal distribution table, we will get:

`P(z>1)=1-0.84134`

`P(z>1)=0.15866`

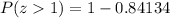
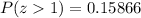
Therefore, the probability that the sample mean is greater than $66,000 would be 0.15866 or approximately
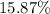`15.87\%`.