Answer:
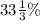
Explanation:
Given:
The average (arithmetic mean) of the 43 numbers in list L is a positive number.
The average of all 48 numbers in both lists L and M is 50 percent greater than the average of the 43 numbers in list L.
Question asked:
What percent greater than the average of the numbers in list L is the average of the numbers in list M?
Solution:
As the total number of observation in both list = 48
And the number of observation in list L = 43
Then, the number of observation in list M = 48 - 43 = 5
Let the average of the 43 numbers in list L = 100
Then the average of all 48 numbers in both lists L and M =
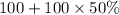
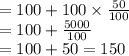
The average of the numbers in list M = 150 - 100 = 50
To find percent greater than the average of the numbers in list L in compare to average of the numbers in list M,
Average of the numbers in list L - average of the numbers in list M divided by the average of all 48 numbers in both lists L and M multiplied by 100
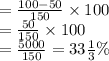
Thus,
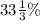 greater than the average of the numbers in list L is the average of the numbers in list M.
greater than the average of the numbers in list L is the average of the numbers in list M.