Question

The distance that an object falls varies directly as the square of the time the object is in motion. If an object falls for 3​ seconds, it will fall 144.9 feet. To estimate the height of a​ cliff, a person drops a stone at the edge of the cliff and measures how long it takes for the stone to reach the base. If it takes 2.3 ​seconds, what is the height of the​ cliff?

Answer 1

85.2 feet

Explanation:

Let the distance be 'd' and time be 't'.

Given:

Distance varies directly as the square of the time the object is in motion.

So,

`d\propto t^2\\\\d=kt^2`

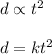
Where, 'k' is constant of proportionality.

Now, also given:

When d = 144.9 ft, t = 3 s

Plug in these value in the above equation to find 'k'. This gives,

`144.9=3^2k\\\\k=(144.9)/(9)=16.1\ ft/s^2`

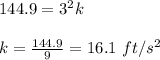
Now, we need to find 'd' when time 't' equals 2.3 s.

So, plug in the given values in the above equation to get the value of 'd'. This gives,

`d=16.1* (2.3)^2\\\\d=16.1* 5.29=85.2\ ft`

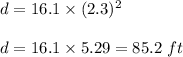
Therefore, the distance traveled by the object to reach base is nothing but the height of cliff. So, height of cliff is 85.2 ft.