Answer:
a) 0.1217 = 12.17% probability that a disk has exactly one missing pulse
b) 0.0089 = 0.89% probability that a disk has at least two missing pulses
c) 0.7559 = 75.59% probability that neither contains a missing pulse
Explanation:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given time interval.
is the mean in the given time interval.
In this problem, we have that:
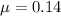
(a) What is the probability that a disk has exactly one missing pulse? (Round to four decimal places)
This is P(X = 1).


0.1217 = 12.17% probability that a disk has exactly one missing pulse
(b) What is the probability that a disk has at least two missing pulses? (Round to four decimal places)
Either a disk had at most 1 one missing pulse, or it had at least two. The sum of the probabilities of these events is 1. So
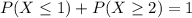
We want
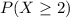 . So
. So
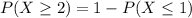
In which
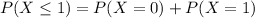

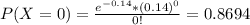

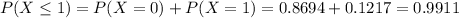
So
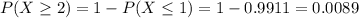
0.0089 = 0.89% probability that a disk has at least two missing pulses
(c) If two disks are independently selected, what is the probability that neither contains a missing pulse?(Round to four decimal places)
Each disk has a 0.8694 probability of having no missing pulses.
Since they are independently selected,
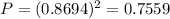
0.7559 = 75.59% probability that neither contains a missing pulse