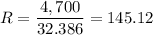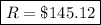Answer:
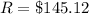
Explanation:
Compound Interest
This is a well-know problem were we want to calculate the regular payment R needed to pay a principal P in n periods with a known rate of interest i.
The present value PV or the principal can be calculated with
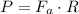
Solving for R
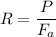
Where Fa is computed by
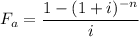
We'll use the provided values but we need to convert them first to monthly payments
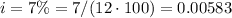
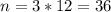
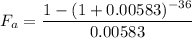
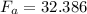
Thus, each payment is