Question

What is the result of substituting for y in the bottom equation
y=x+3
y=x^2+2x-4

Answer 1

The solutions are (2.1925, 5.1925) and (-3.1925, -0.1925)

Solution:

Given that,

`y = x + 3 ------- eqn 1\\\\y = x^2 + 2x - 4 ----- eqn 2`

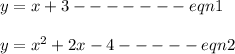
We have to substitute eqn 1 in eqn 2

`x + 3 = x^2 + 2x - 4`

`\mathrm{Switch\:sides}\\\\x^2+2x-4=x+3\\\\\mathrm{Subtract\:}3\mathrm{\:from\:both\:sides}\\\\x^2+2x-4-3=x+3-3\\\\\mathrm{Simplify}\\\\x^2+2x-7=x\\\\\mathrm{Subtract\:}x\mathrm{\:from\:both\:sides}\\\\x^2+2x-7-x=x-x\\\\\mathrm{Simplify}\\\\x^2+x-7=0`

`\mathrm{Solve\:with\:the\:quadratic\:formula}\\\\\mathrm{For\:a\:quadratic\:equation\:of\:the\:form\:}ax^2+bx+c=0\mathrm{\:the\:solutions\:are\:}\\\\x=(-b\pm √(b^2-4ac))/(2a)\\\\\mathrm{For\:}\quad a=1,\:b=1,\:c=-7\\\\x =(-1\pm √(1^2-4\cdot \:1\left(-7\right)))/(2\cdot \:1)`

`x = (-1 \pm √( 1 + 28))/(2)\\\\x = ( -1 \pm √(29))/(2)`

`x = ( -1 \pm 5.385 )/(2)\\\\We\ have\ two\ solutions\\\\x = ( -1 + 5.385 )/(2)\\\\x = 2.1925`

`Also\\\\x = ( -1 - 5.385 )/(2)\\\\x = -3.1925`

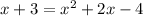
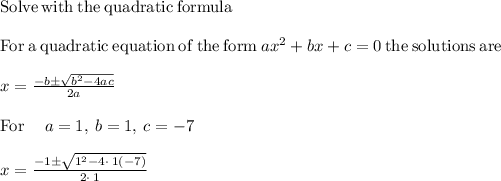
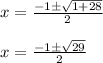
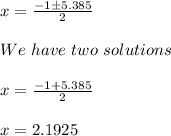
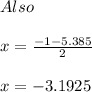
Substitute x = 2.1925 in eqn 1

y = 2.1925 + 3

y = 5.1925

Substitute x = -3.1925 in eqn 1

y = -3.1925 + 3

y = -0.1925

Thus the solutions are (2.1925, 5.1925) and (-3.1925, -0.1925)