Question

In the coordinate plane the vertices of rst are: r(6 -1), s (1 -4), t (-5,6). Prove that rst is a right triangle. State the coordinates of p such that quadrilateral rstp is a rectangle.

Answer 1

Triangle RST is proven to be a right triangle by demonstrating that the Pythagorean theorem holds true for the lengths of its sides. Point P should be at coordinates (-5, -1) to form rectangle RSTP.

Step-by-step explanation:

To prove that triangle RST with vertices R(6, -1), S(1, -4), and T(-5, 6) is a right triangle, we must show that one of the angles in the triangle is a right angle. We can do this by demonstrating that the square of the length of one side is equal to the sum of the squares of the lengths of the other two sides (Pythagorean Theorem). First, we find the lengths of the sides by calculating the distances between the vertices:

• RS: √[(1 - 6)^2 + (-4 - (-1))^2] = √[25 + 9] = √34
• ST: √[(-5 - 1)^2 + (6 - (-4))^2] = √[36 + 100] = √136
• RT: √[(-5 - 6)^2 + (6 - (-1))^2] = √[121 + 49] = √170

Now, let's check if the Pythagorean theorem holds for any two sides as the legs and the third as the hypotenuse.

• (√34)^2 + (√136)^2 = 34 + 136 = 170
• (√170)^2 = 170

Since the squares of the lengths of RS and ST sum up to the square of the length of RT, this indicates that ∠RST is a right angle, and hence RST is a right triangle.

To make quadrilateral RSTP a rectangle, point P must be directly opposite to the right angle vertex R across the diagonal SP, and it must also make SP a diagonal of the rectangle. Since rectangles have congruent opposite sides and right angles, the coordinates of P will be P(-5, -1). This maintains the same x-coordinate as point T and the same y-coordinate as point R to ensure that the new sides SP and RP are parallel to the existing sides ST and RS, respectively.

Answer 2

Coordinates of point p: (0,9)

Step-by-step explanation:

We have been given that in the coordinate plane the vertices of rst are: r (6, -1), s (1, -4), t (-5,6). We are asked to prove that rst is a right triangle.

First of all, we will find the slope between points 'r' and 's' and 's' and 't'.

`\text{Slope}_(rs)=(-1-(-4))/(6-1)=(-1+4)/(5)=(3)/(5)`

`\text{Slope}_(st)=(-4-6)/(1-(-5))=(-10)/(1+5)=-(10)/(6)=-(5)/(3)`

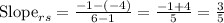
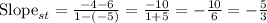
We know that slope of perpendicular lines in negative reciprocal of each other.

Let us find the product of both slopes.

`(3)/(5)* (-5)/(3)=-1`

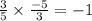
Since product of both slopes is
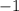`-1`, therefore, line 'rs' is perpendicular to line 'st' and 'rst' is a right triangle.

Let us assume that coordinates of point p are
`(x,y)`.

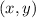We need to find slope of point 'r' to 'p' is equal to slope of point 's' to point 't' and slope of point 'p' to 't' is equal to slope of point 'r' to point 's'.

`\text{Slope}_(rp)=(-1-y)/(6-x)=-(5)/(3)`

`\text{Slope}_(pt)=(y-6)/(x-(-5))=(3)/(5)`

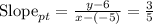
Now, we have two equations and two unknown.

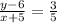`(y-6)/(x+5)=(3)/(5)` and
`(-1-y)/(6-x)=-(5)/(3)`

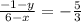
To solve our system, we will use substitution method.

`y=(3)/(5)(x+5)+6`

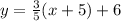
Upon substituting this value in equation (2), we will get:

`(-1-((3)/(5)(x+5)+6))/(6-x)=-(5)/(3)`

`(-(5)/(5)-(3)/(5)(x+5)-(30)/(5))/(6-x)=-(5)/(3)`

`((-5-3x-15-30)/(5))/(6-x)=-(5)/(3)`

`(-50-3x)/(5(6-x))=-(5)/(3)`

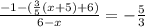
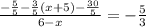
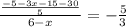
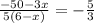
Cross multiply:

`3(-50-3x)=-25(6-x)`

`-150-9x=-150+25x`

`-9x=25x`

`-9x+9x=25x+9x`

`34x=0`

`x=0`

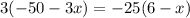
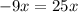
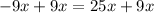
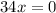
Upon substituting
`x=0` in equation
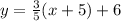`y=(3)/(5)(x+5)+6`, we will get:

`y=(3)/(5)(0+5)+6`

`y=(3)/(5)(5)+6`

`y=3+6=9`

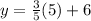
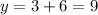
Therefore, the coordinates of point p at (0,9) that will make quadrilateral rstp is a rectangle.