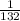Question

There are 12 balls in a bag. One is blue and one is red. What is the exact probability that the blue ball is drawn first and the red ball is drawn second? (Without replacement)

Answer 1

The exact probability that the blue ball is drawn first and the red ball is drawn second is
`(1)/(132)`

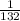
Solution:

The probability of an event is given as:

`Probability = \frac{ \text{ number of favorable outcomes }}{ \text{ total number of possible outcomes }}`

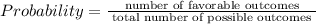
Given that,

There are 12 balls in a bag

One is blue and one is red

Favorable outcome = blue ball is drawn first

Favorable outcome = 1

Therefore,

`Probability = (1)/(12)`

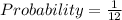
Now, without replacement, red ball is drawn second

Therefore,

Total possible outcomes = 12 - 1 = 11

`Probability = (1)/(11)`

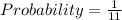
What is the exact probability that the blue ball is drawn first and the red ball is drawn second?

`Total\ probability = (1)/(12) * (1)/(11) = (1)/(132)`

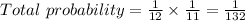
Thus the exact probability that the blue ball is drawn first and the red ball is drawn second is
`(1)/(132)`