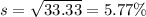Question

Ford Motor Company had realized returns of 15%, 25%, 25%, and 15% over four quarters.

What is the quarterly standard deviation of returns for Ford calculated from this sample?

Answer 1

`\bar X = (\sum_(i=1)^n X_i)/(n)`

And replacing we got:

`\abr X = (15+25+25+25)/(4)= 20 \%`

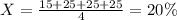
And now we can calculate the variance like this:

`s^2 = ((15-20)^2 +(25-20)^2 +(25-20)^2 +(15-20)^2)/(4-1)= (100)/(3)= 33.33`

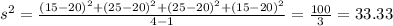
And the deviation is just the square root of the variance and we got:

`s = √(33.33)= 5.77 \%`

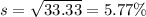
Step-by-step explanation:

For this case we have the following data:

15%, 25%, 25%, and 15%

So for this case n = 4

And we can calculate the sample variance with the following formula:

`s^2 = (\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)`

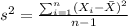
First we need to calculate the mean with this formula:

`\bar X = (\sum_(i=1)^n X_i)/(n)`

And replacing we got:

`\abr X = (15+25+25+25)/(4)= 20 \%`

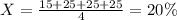
And now we can calculate the variance like this:

`s^2 = ((15-20)^2 +(25-20)^2 +(25-20)^2 +(15-20)^2)/(4-1)= (100)/(3)= 33.33`

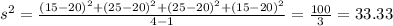
And the deviation is just the square root of the variance and we got:

`s = √(33.33)= 5.77 \%`