Question

What is 2 log Subscript 5 Baseline (5 x cubed) + one-third log Subscript 5 Baseline (x squared + 6) written as a single logarithm?

Answer 1

B

Explanation:

Answer 2

Answer:
`log_5(25x^6\sqrt[3]{ x^2+6})`

Explanation:

Given the following expression:

`2log_5(5x^3)+(|)/(3)log_5(x^2+6)`

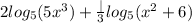
You need to remember the following properties for Logarithms:

`1.\ log(a)+log(b)=log(ab)\\\\2.\ log(a)-log(b)=log((a)/(b))\\\\3.\ log(a)^n=nlog(a)`

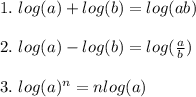
And the following property for Radicals:

`a^{(1)/(n)}=\sqrt[n]{a}`

According to the Power of a power property:

`(a^m)^n=a^(mn)`

Then, you can follow these steps:

Step 1: Apply the third property for logarithms shown above:

`=log_5(5x^3)^2+log_5(x^2+6)^{(1)/(3)}`

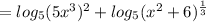
Step 2: Apply the Power of a power property:

`=log_5(25x^6)+log_5(x^2+6)^{(1)/(3)}`

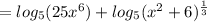
Step 3: Using the property for Radicals shown before:

`=log_5(25x^6)+log_5(\sqrt[3]{ x^2+6})`

Step 4: Now you must apply the first property for logarithms:

`=log_5(25x^6\sqrt[3]{ x^2+6})`