What is the rate of change for a linear function that passes through the points (8, -10) and (-6, 14)

Question

asked Dec 28, 2021 23.2k views

2 Answers

Priyanka Sankhala · Answer 1 · 2022-01-02T07:36:35+0000

Answer:
m=-1.714

Explanation:

By definition, the slope of the line is described as "Rate of change".

You need to use the following formula to calcualte the slope of the line;

m=(y_2-y_1)/(x_2-x_1)

In this case you know that the line passes through these two points: (8, -10) and (-6, 14).

Then, you can say that:

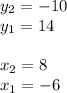
$y_2=-10\\y_1=14\\\\x_2=8\\x_1=-6$

Knowing these values, you can substitute them into the formula for calculate the slope of a line:

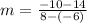
m=(-10-14)/(8-(-6))

Finally, you must evaluate in order to find the slope of this line. You get that this is:

$m=(-24)/(8+6)\\\\m=(-24)/(14)\\\\m=-(12)/(7)\\\\m=-1.714$