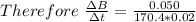Question

A 170.4-turn circular loop of radius 0.08 meters with a magnetic field B passing through the area bounded by the loop at right angles has an Emf of 0.050 Volts induced around the loop by the rising magnetic field. How fast is the magnetic field rising in tesla per second

Answer 1

The speed of the magnetic field rising is
`(\Delta B)/(\Delta t)`
`=0.0147 \ T/s`

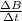
Step-by-step explanation:

Mathematically Induced Emf is as follows

`e = - (\Delta B)/(\Delta t) *N * Area`

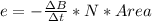
The objective of this solution is to obtain speed in Tesla per second which the same as
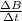`(\Delta B)/(\Delta t)` since the unit of magnetic field B is Tesla and Time is seconds

So making
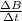`(\Delta B)/(\Delta t)` the subject

`(\Delta B)/(\Delta t ) =(Emf)/(N*Area)`

`The \ Area = \pi r^2`

`= 3.142 * (0.08)^2`

`=0.020m`

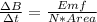
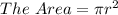
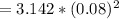
N is given as 170.4 turns

`Therefore \ (\Delta B)/(\Delta t) = (0.050)/(170.4*0.02)`

`=0.0147 \ T/s`