Answer:
There is not enough evidence to support the claim that more than 50% of the observations in a population are below 10
Explanation:
We are given the following in the question:
8, 12, 5, 9, 14, 11, 12, 6, 8, 9, 2, 6, 11, 9, 3, 7, 8, 4, 13, 10
Sample size, n = 20
p = 50% = 0.50
Alpha, α = 0.05
Observations below 10,x = 13
First, we design the null and the alternate hypothesis
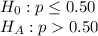
This is a one-tailed(right) test.
Formula:
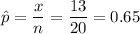
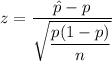
Putting the values, we get,
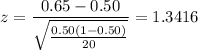
Now, we calculate the p-value from the table.
P-value = 0.08986
Since the p-value is greater than the significance level, we fail to reject the null hypothesis and accept the null hypothesis.
Thus, there is not enough evidence to support the claim that more than 50% of the observations in a population are below 10