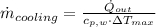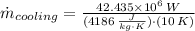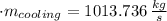Question

Steam enters the condenser of a steam power plant at 20 kPa and a quality of 95 % with a mass flow rate of 20,000 kg/h. It is to be cooled by water from a nearby river by circulating the water through the tubes within the condenser. To prevent thermal pollution, the river water is not allowed to experience a temperature rise above 10 ºC. If the steam is to leave the condenser as saturated liquid at 20 kPa, determine the mass flow rate of the cooling water required.

Answer 1

Step-by-step explanation:

The steam enters the condenser as a vapor-liquid mix and exits as a saturated liquid. Specific enthalpies at inlet and outlet are given from a property table for saturated water:

Inlet

`h_(in) = h_(f) + x\cdot (h_(fg))`

`h_(in) = 251.42\,(kJ)/(kg) + 0.95\cdot (2357.5\,(kJ)/(kg) )`

`h_(in) = 2373.17\,(kJ)/(kg)`

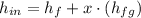
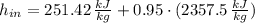
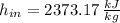
Outlet

`h_(out) = h_(f)`

`h_(out) = 251.42\,(kJ)/(kg)`

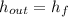
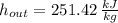
The heat transfer rate to the river is:

`\dot Q_(out) = \dot m_(steam)\cdot (h_(in) - h_(out))`

`\dot Q_(out) = (20000\,(kg)/(s) )\cdot (2373.17\,(kJ)/(kg)-251.42\,(kJ)/(kg) )`

`\dot Q_(out) = 42.435* 10^(6)\,W`

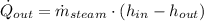
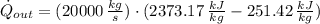
The mass flow rate of the cooling water is:

`\dot m_(cooling) = (\dot Q_(out))/(c_(p,w)\cdot \Delta T_(max))`

`\dot m_(cooling) = (42.435* 10^(6)\,W)/((4186\,(J)/(kg\cdot K) )\cdot (10\,K))`

`\cdot m_(cooling) = 1013.736\,(kg)/(s)`