Question

A 6500 kg satellite orbits a planet. If its distance to the center of the planet is 9e6 m and its speed is 6.7e3 m/s, what is the gravitational force between the satellite and the planet

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

Option D is the Answer

Step-by-step explanation:

The formula for the velocity of the satellite is

`v =\sqrt{(GM)/(R) }`

R is the distance to the center o the planet =
`9*10^6m`

G is the gravitational constant which is equal to
`= 6.67*10^(-11) (Nm^2)/(kg^2)`

M is the mass of the planet

Making M the subject of the formula we have

`M = ((v^2)(R))/(G)`

`M = ((6.7*10^3)^2(9*10^6))/(6.67*10^(-11)) = 60.57*10^(23)Kg`

The formula for the gravitational force between two object

`F = (GMm)/(R^2)`

Where

`= (6.67*10^(-11)(6.057*10^(24))(6500))/((9*10^6)^2)`

`F = 32,419.90 N`

`= 3.24*10^(4) N`

Answer 2

the gravitational force between the satellite and the planet is 32.4 * 10³N

Step-by-step explanation:

It is given that,

Mass of the satellite, m = 6500 kg

Speed of the satellite, v = 6.7 × 10³ m/s

distance to the center of the planet = 9 × 10⁶m

Let F is the magnitude of the gravitational force exerted on the satellite by the planet. The centripetal force is equal to the gravitational force. It is equal to :

`F = (mv^2)/(R)`

`F = (6500 * (6.7 * 10^3))/(9 * 10^6)`

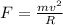
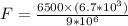
= 32.4 * 10³N

the gravitational force between the satellite and the planet is 32.4 * 10³N