Question

A boy shoves his stuffed toy zebra down a frictionless chute. It starts at a height of 1.69 m above the bottom of the chute with an initial speed of 1.23 m/s . The toy animal emerges horizontally from the bottom of the chute and continues sliding along a horizontal surface with a coefficient of kinetic friction of 0.255 . How far from the bottom of the chute does the toy zebra come to rest

Answer 1

6.45m

Step-by-step explanation:

See the attachments below

Answer 2

x = 6.94 m

Step-by-step explanation:

For this exercise we can find the speed at the bottom of the ramp using energy conservation

Starting point. Higher

Em₀ = K + U = ½ m v₀² + m g h

Final point. Lower

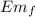`Em_(f)` = K = ½ m v²

Em₀ = Em_{f}

½ m v₀² + m g h = ½ m v²

v² = v₀² + 2 g h

Let's calculate

v = √(1.23² + 2 9.8 1.69)

v = 5.89 m / s

In the horizontal part we can use the relationship between work and the variation of kinetic energy

W = ΔK

-fr x = 0- ½ m v²

Newton's second law

N- W = 0

The equation for the friction is

fr = μ N

fr = μ m g

We replace

μ m g x = ½ m v²

x = v² / 2μ g

Let's calculate

x = 5.89² / (2 0.255 9.8)

x = 6.94 m