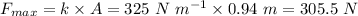Answer:
Part(a): The amplitude of motion is 0.94 m.
Part(b): The maximum acceleration of the block is 165.13
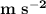 .
.
Part(c): The maximum force that the spring exerts on the block is 305.5 N.
Step-by-step explanation:
Part(a):
Given the mass (
 ) of the block is 1.85 Kg, the force constant (
) of the block is 1.85 Kg, the force constant (
 ) is 325
) is 325
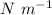 .Initially the spring is neither stretched nor compressed, which indicates that the block at this situation is in its equilibrium position where the maximum velocity of the block is
.Initially the spring is neither stretched nor compressed, which indicates that the block at this situation is in its equilibrium position where the maximum velocity of the block is
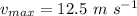 . If '
. If '
 ' be the amplitude of motion, then the velocity of the particle executing simple harmonic motion at any instant of position (
' be the amplitude of motion, then the velocity of the particle executing simple harmonic motion at any instant of position (
 ) is
) is

where
 is the natural angular frequency.
is the natural angular frequency.
At equilibrium position, x = 0. So, the maximum velocity (
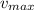 ), using equation (I) can be written as
), using equation (I) can be written as
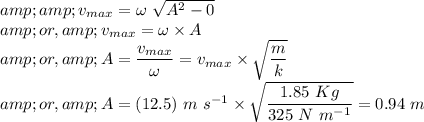
Part(b):
The acceleration (
 ) of a particle executing SHM is given by
) of a particle executing SHM is given by

The block will gain its maximum acceleration when it is at a distance equal to its amplitude. SO from equation (II), the maximum acceleration (
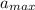 ) of the block is
) of the block is
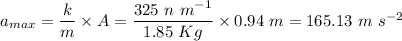
Part(c):
The block will experience a maximum restoring force (
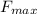 ) when it is at a distance
) when it is at a distance
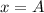 . So, the value of the maximum force is
. So, the value of the maximum force is