Question

A 6.00 μFμF capacitor that is initially uncharged is connected in series with a 4.00 ΩΩ resistor and an emf source with EE EMF = 60.0 V and negligible internal resistance.The circuit is completed at t = 0. (a) Just after the circuit is completed, what is the rate at which electrical energy is being dissipated in the resistor? (b) At what value of t is the rate at which electrical energy is being dissipated in the resistor equal to the rate at which electrical energy is being stored in the capacitor? (c) At the time calculated in part (b), what is the rate at which electrical energy is being dissipated in the resistor?

Answer 1

Complete Question

A 6.00 μFμF capacitor that is initially uncharged is connected in series with a 4.00 kΩ resistor and an emf source with EE EMF = 60.0 V and negligible internal resistance.The circuit is completed at t = 0. (a) Just after the circuit is completed, what is the rate at which electrical energy is being dissipated in the resistor? (b) At what value of t is the rate at which electrical energy is being dissipated in the resistor equal to the rate at which electrical energy is being stored in the capacitor? (c) At the time calculated in part (b), what is the rate at which electrical energy is being dissipated in the resistor?

Answer:

a

The rate at which electrical energy is being dissipated in the resistor is
`P_R=(60^2)/(4000) =0.9W`

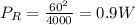
b

The value of time is t = 0.017 sec

c

The energy dissipated at the time obtained in part B is
`P_R = 29.54 W`

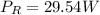
Step-by-step explanation:

The diagram of the circuit when it is open is shown i.e
`t = 0^-` where
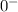`0^-` indicates that the capacitor is uncharged

Since initially the capacitor is not charged

The voltage
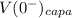`V(0^-)_(capa)` = 0 V

The diagram of the circuit when it is closed here
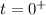`t =0^+` where
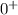`0^+` indicates that the capacitor is charging

The voltage across capacitor would at the point of closing the circle be equal to zero since it can not change instantaneously

Hence
`v_(capa) (0^+) =0 V`

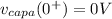
The initial current would be

`i^+ = (E)/(R)`

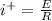
Now at
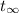`t_\infty` that is when the capacitor is fully charged in an ideal circuit it would then act as an open circuit meaning that the voltage across it would be

`v_(capa) (\infty) = E`

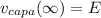
The mathematical relation to obtain the voltage across the capacitor at any point is

`v_(capa) = v_(capa) + (v_(capa)(0^+)-v_(capa)(\infty))e^(-t/RC)`

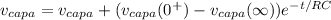
Substituting values

`v_(capa) = E + (0-E)e^(-t/RC)`

`v_(capa) = E (1-e^(-t/RC)) Volt ----(1)`

And since the current is directly proportional to voltage

The mathematical relation to obtain the current through the capacitor at any point is

`i = i(0^+)e^(-t/RC)`

`i = (E)/(R)e^(-t/RC)----(2)`

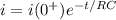
The energy dissipated is mathematically,

`P_R = (E^2)/(R)`

`=(60^2)/(4000) =0.9W`

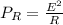
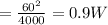
The energy loss in the lost in the resistor is Mathematically given as

`P_R = i^2R`

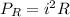
Now the energy dissipated at the capacitor is Mathematically given as

`P_c = (q*i)/(C)`

Equating the both energies

`(q*i)/(C) = i^2R`

=>
`i =(q)/(RC) ---(3)`

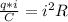
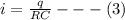
Mathematically the q stored on the capacitor is

`q = C v_(capa)`

`=EC(1-e^(-t/RC))`

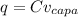
And from Eqn(2)

`i = (E)/(R) e^(-t/RC)`

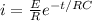
Substituting i and q into Eqn(3)

`(E)/(R)e^(-t/RC) = (EC(1-e^(-t/RC)))/(RC)`

`e^(-t/RC) = 1- e^(-t/RC)`

`2e^(-t/RC) = 1`

`e^(-t/RC) = 0.5`

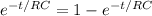
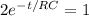
Taking natural log of both sides

`-(t)/(RC) =ln(0.5)`

Substituting the values given for resistance and capacitor

`-(t)/((6.0*10^(-6))(4000)) = -0.693`

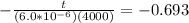
t = 0.017 sec

Considering the equation for the energy dissipated in the resistor

`P_R =i^2 R`

`i = (E)/(R) e^(-t/RC)`

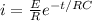
Substituting values

`i = (60)/(4000)e^{-0.017/(6*10^(-6)*4000)}`

`=0.0074A`

`P_R = (0.007)^2 * 4000`

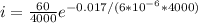
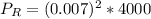
= 29.54 W

Answer 2

Answer: Rr = 900w

T = 1.66×10^-5s

P = 36.92W

Explanation: please find the attached file for the solution.