Question

The count in a bacteria culture was 100 after 20 minutes and 2000 after 40 minutes. Assuming the count grows exponentially, What was the initial size of the culture? Find the doubling period. Find the population after 65 minutes. When will the population reach 12000. Submit Question

Answer 1

Step-by-step explanation:

Let X be the number of bacteria at time t, and Xo be the initial number of bacteria

Bacteria grows exponentially, the exponential growth model is thus:

X = Xo
`e^(kt)`

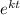
[e is the exponential sign]

k is the growth constant = growth rate

At t = 20 minutes, X = 100

At t = 40 minutes, X = 2000

Substituting that into the formula

(i) ... 100 = Xo
`e^(k20)`

(ii) ... 2000 = Xo
`e^(k40)`

Divide (ii) by (i)

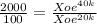
`(2000)/(100) = \frac{Xoe^(40k) } {Xoe^(20k)}`

20 =
`e^(40k-20k) = e^(20k)`

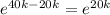
[Xo cancels Xo. Division of values raised to a power is done by subtracting their powers]

Take the natural log of both sides

㏑20 = 20k

[taking the ㏑ cancels the exponential]

k =
`(ln20)/(20)`

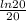
We can now substitute k to solve one of the equations

substituting k in (ii): 2000 = Xo
`e(ln 20)/(20).^(40)`

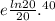
2000 = Xo
`e^(0.15*40)`

2000 = Xo
`e^(6)`

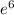
Making Xo the subject of the formula

Xo =
`(2000)/(e^(6) )`

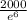
Xo is approximately 5 cells.

THE DOUBLING TIME

The doubling time is the time it takes for the population to double, so 5 cells become 10 cells

Since Xo = 5

Given that X = Xo
`e^(kt)`

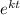
When X=10,

10 = 5
`e^(0.15t)`

solving for t:

`e^(0.15t) = (10)/(5)`

Take ln of both sides

0.15t = ln 2

t =
`(ln2)/(0.15)`

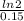
t =4.62 minutes

POPULATION AFTER 65 MINUTES

X = 5
`e^(0.15*65)`

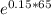
X = 85770

WHEN WILL THE POPULATION REACH 12000

12000 = 5
`e^(0.15t)`

`e^(0.15t)` =240

take ln of both sides

0.15t = ln 2400

t = 51.89 minutes (approximately 52 minutes)