Given Data:
At distance d₁ = 4.5×10¹⁰ m, speed of comet is
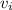 = 9.2×10⁴ m/s.
= 9.2×10⁴ m/s.
At distance d₂ = 6×10¹² m, speed of comet will be
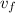 = ?
= ?
As there is no work done from the outside, so the initial energy of the system will be equal to the final state of energy.


![v_(f) = \sqrt{v^(2) _(i)+2GM[(1)/(d_(2)) -(1)/(d_(1) ) ] }](https://img.qammunity.org/2021/formulas/geography/college/ebnhn84172oxje9zgp8t1qp8lpy5uvii54.png)
Now by putting the values in the above equation we can find out
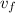 . Here M is the mass of sun.
. Here M is the mass of sun.
![v_(f) = \sqrt{(9.2*10^(4))^(2) + 2(6.7*10^(-11))(1.98*10^(30))[(1)/(6*10^(12))-(1)/(4.5*10^(10) ) } } ]](https://img.qammunity.org/2021/formulas/geography/college/7mx7we2dfr1gkdfsa2su0d8cckyla110ts.png)
= 51109.88 m/s