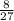The value of y is
Step-by-step explanation:
Given that y varies directly as x and inversely as the square of z.
Thus, it can be written as
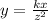
Also, given that
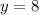 when
when
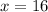 and
and
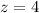
Substituting these values in the above expression, we have,
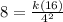
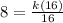
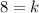
Thus, the value of the constant is 8
Now, we shall find the value of y.
The value of y can be determined by substituting
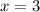 ,
,
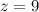 and
and
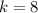 in the expression
in the expression
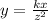
Thus, we have,
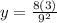
Simplifying, we get,

Dividing, we get,
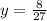
Thus, the value of y is