Answer:
t = 3.016
P-value = 0.0061
Explanation:
Let us assume that the population variance is unequal
Null hypothesis :
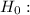 μ
μ
 = μ
= μ

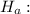 μ
μ
 ≠ μ
≠ μ

The alternative hypothesis :
Here we have
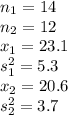
Since it is not given that variances are equal, degrees of freedom of the test is given as
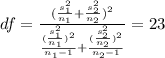
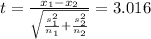
The P-value of the test is = 0.0061
Since the p-value is less than 0.05, we will reject the null hypothesis