Answer:
Tarzan will knock her off her limb. (CRASH!)
Step-by-step explanation:
The difference between a tender embrace or a knock out is derived of a convenient application of the Principle of Energy Conservation, in which a tender embrace mean the absence of kinetic energy and, most specific, speed, when Tarzan arrives to the tree, where Jane is waiting. Tarzan starts at rest. Hence:
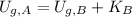
The criteria is depicted as follows:
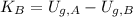


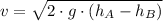
Heights are, respectively:
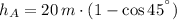
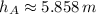
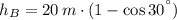
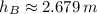
The final speed is:
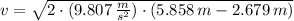

Which mean that Tarzan will knock her off her limb. (CRASH!)