Question

Sometimes, when the wind blows across a long wire, a low-frequency "moaning" sound is produced. The sound arises because a standing wave is set up on the wire, like a standing wave on a guitar string. Assume that a wire (linear density = 0.0190 kg / m ) sustains a tension of 365 N because the wire is stretched between two poles that are 6.93 m apart. The lowest frequency that an average, healthy human ear can detect is 20.0 Hz. What is the lowest harmonic number n that could be responsible for the "moaning" sound?

Answer 1

`n = 2`

Step-by-step explanation:

Lets see the given parameters.

Length of wire (L) = 6.93

Linear Density of wire (m/L) = 0.019 kg/m

Tension Force (F) = 365 Newtons

Now, the fundamental frequency (
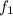`f_1`) of the wire is given by the formula:

`f_1=(1)/(2L)\sqrt{(F)/(m/L)}`

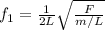
Where

L is length of wire

F is the tension force

m/L is the linear density

Plugging in, we get:

`f_1=(1)/(2L)\sqrt{(F)/(m/L)}\\f_1=(1)/(2*6.93)\sqrt{(365)/(0.0190)}\\f_1=10.007`

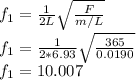
We can say the fundamental frequency to be about 10 Hz

Now, we know that the lowest frequency humans can hear is 20 Hz.

The lowest harmonic number is gotten by dividing this by the fundamental frequency:

20/10 = 2

Thus,

n = 2