Question

Two waves have the same speed. The first has twice the frequency of the second. Compare the wavelength of the two waves. 1. The first has half the wavelength of the second. 2. The second has half the wavelength of the first. 3. They have the same wavelength. 4. The second has one third the wavelength of the first. 5. The first has one third the wavelength of the second.

Answer 1

1. The first has half the wavelength of the second

Step-by-step explanation:

Consider λ₁ and λ₂ be the wavelengths of the first and second wave respectively.

Consider f₁ be the frequency of the first wave. According to the problem,

Frequency of the second wave, f₂ = f₁/2 ....(1)

The relation between speed, frequency and wavelength of the wave is:

v = λf

Here v is speed of the wave, λ is wavelength and f is frequency.

So, the speed of first wave is:

v₁ = λ₁f₁

And, speed of second wave is:

v₂ = λ₂f₂

But according to the problem:

v₁ = v₂

λ₁f₁ = λ₂f₂

`(\lambda_(1) )/(\lambda_(2) )=(f_(2) )/(f_(1) )`

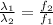
Put equation (1) in the above equation.

`(\lambda_(1) )/(\lambda_(2) )=(f_(1) )/(2f_(1) )`

`(\lambda_(1) )/(\lambda_(2) )=(1)/(2)`

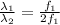
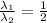
λ₂ = 2λ₁ or λ₁ = λ₂/2