Question

Out of the students in a class, 50% are geniuses, 60% love chocolate, and 30% fall into both categories. Determine the probability that a randomly selected student from the class is neither a genius nor a chocolate lover.

Answer 1

20% probability that a randomly selected student from the class is neither a genius nor a chocolate lover.

Explanation:

We solve this problem building the Venn's diagram of these probabilities.

I am going to say that:

A is the probability that a student is a genius.

B is the probability that a men student likes chocolate.

C is the probability that a student is not a genius and does not like chocolate.

We have that:

`A = a + (A \cap B)`

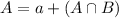
In which a is the probability that a student is a genius but does not like chocolate and
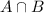`A \cap B` is the probability that a student is both a genius and likes chocolate.

By the same logic, we have that:

`B = b + (A \cap B)`

30% fall into both categories.

This means that
`A \cap B = 0.3`

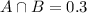
60% love chocolate

This means that
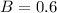`B = 0.6`. So

`B = b + (A \cap B)`

`0.6 = b + 0.3`

`b = 0.3`

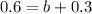
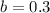
50% are geniuses

`A = a + (A \cap B)`

`0.5 = a + 0.3`

`a = 0.2`

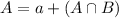
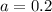
We know that either a student is at least a genius or likes chocolate, or a student is not a genius and does not like chocolate. The sum of the probabilities of these events is decimal 1. So

`(A \cup B) + C = 1`

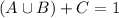
In which

`A \cup B = a + b + (A \cap B) = 0.2 + 0.3 + 0.3 = 0.8`

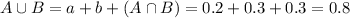
We want C, so

`(A \cup B) + C = 1`

`0.8 + C = 1`

`C = 0.2`

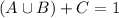
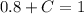
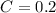
20% probability that a randomly selected student from the class is neither a genius nor a chocolate lover.