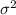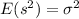Question

A sample of 5 buttons is randomly selected and the following diameters are measured in inches. Give a point estimate for the population variance. Round your answer to three decimal places. 1.04,1.00,1.13,1.08,1.11

Answer 1

`s^2 = (\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)`

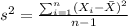
But we need to calculate the mean with the following formula:

`\bar X = (\sum_(i=1)^n X_I)/(n)`

And replacing we got:

`\bar X = ( 1.04+1.00+1.13+1.08+1.11)/(5)= 1.072`

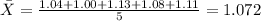
And for the sample variance we have:

`s^2 = ((1.04-1.072)^2 +(1.00-1.072)^2 +(1.13-1.072)^2 +(1.08-1.072)^2 +(1.11-1.072)^2)/(5-1)= 0.00277\ approx 0.003`

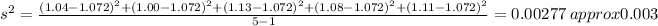
And thi is the best estimator for the population variance since is an unbiased estimator od the population variance
`\sigma^2`

`E(s^2) = \sigma^2`

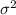
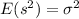
Explanation:

For this case we have the following data:

1.04,1.00,1.13,1.08,1.11

And in order to estimate the population variance we can use the sample variance formula:

`s^2 = (\sum_(i=1)^n (X_i -\bar X)^2)/(n-1)`

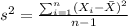
But we need to calculate the mean with the following formula:

`\bar X = (\sum_(i=1)^n X_I)/(n)`

And replacing we got:

`\bar X = ( 1.04+1.00+1.13+1.08+1.11)/(5)= 1.072`

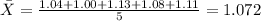
And for the sample variance we have:

`s^2 = ((1.04-1.072)^2 +(1.00-1.072)^2 +(1.13-1.072)^2 +(1.08-1.072)^2 +(1.11-1.072)^2)/(5-1)= 0.00277\ approx 0.003`

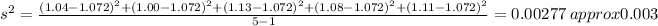
And thi is the best estimator for the population variance since is an unbiased estimator od the population variance
`\sigma^2`

`E(s^2) = \sigma^2`